후크의 법칙과 단순 조화 운동
English
Share
Overview
출처: 케트론 미첼 윈, 박사, 아산타 쿠레이, 박사, 물리학 및 천문학, 물리 과학 학교, 캘리포니아 대학, 어바인, 캘리포니아
잠재적인 에너지는 물리학에서 중요한 개념입니다. 잠재적 에너지는 주변 을 기준으로 물체의 위치에 의존하는 힘과 관련된 에너지입니다. 다른 비디오에서 논의되는 중력 잠재적 에너지는 지상 물체의 높이에 직접적으로 비례하는 에너지입니다. 마찬가지로, 스프링 잠재 에너지를 정의할 수 있으며, 이는 완화된 상태에서 스프링의 변위에 직접적으로 비례합니다. 늘거나 압축된 스프링은 물체에 대한 작업을 수행할 수 있기 때문에 잠재적인 에너지를 가지고 있습니다. “일을 할 수있는 능력”은 종종 에너지의 기본 정의로 인용됩니다.
이 비디오는 스프링에 저장된 잠재적 인 에너지를 보여줍니다. 또한 스프링의 복원 력 방정식 또는 Hooke의 법칙을 확인합니다. 스프링 상수는 다른 탄성의 스프링에 대해 다릅니다. Hooke의 법칙은 검증되고 스프링 상수는 중단된 스프링에 다양한 가중치를 부착하고 결과 변위를 측정하여 측정됩니다.
Principles
Procedure
Results
Representative results of the experiment, conducted with a spring of constant k = 10 N/m, are shown in Table 1. The plot of F versus the displacement Δy is plotted below in Figure 2. The linear function is fit with a line, and the slope of the line is equal to the spring constant, within a margin of error. The linearity of the result shows the validity of Hooke’s law (Equation 1).
Inspect Table 1 to see how the period T of oscillation is related to the mass that is attached to the spring. The heavier the mass attached to the spring, the longer the period will be, as it is proportional to the square root of the mass (Equation 5). Also, note that when a larger mass is attached to the end of the spring, the spring will be stretched further. The potential energy of the system is larger, as it is a function of the squared displacement from equilibrium (Equation 7). It makes sense that the period is longer for a larger mass—because the spring is displaced further from equilibrium, it will take longer to travel that longer distance.
Table 1. Results.
| Mass (kg) | Weight / F (N) | Δy (m) | PE (J) | T measured (s) | T calculated (s) |
| 0.5 | 4.9 | 0.49 | 2.4 | 1.3 | 1.4 |
| 0.75 | 7.4 | 0.74 | 5.4 | 1.6 | 1.7 |
| 1 | 9.8 | 0.98 | 9.6 | 1.9 | 1.9 |
| 1.5 | 14.7 | 1.5 | 21.6 | 2.5 | 2.4 |
| 2 | 19.6 | 2 | 38.4 | 2.9 | 2.8 |
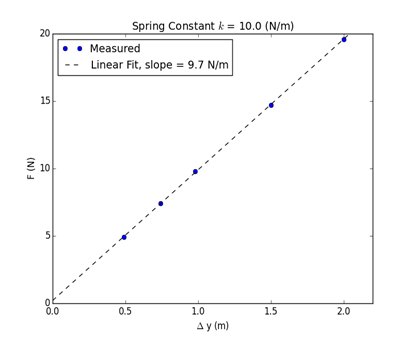
Figure 2: Plot of applied force (N) versus displacement.
Applications and Summary
The use of springs is ubiquitous in our everyday lives. The suspension of modern cars is made from springs that are properly damped. This requires knowledge of the spring constants. For smoother Cadillac rides, springs with a lower spring constant are used, and the ride is “mushier.” High-performance cars use springs with a higher spring constant for better handling. Diving boards are also made with springs of different spring constants, depending upon how much “bounce” is desired when diving off the board. Rock climbing ropes are also slightly elastic, so if a climber falls while climbing, the rope will not only save her from hitting the ground, but it will also dampen the fall with its elasticity. The smaller the spring constant of a climbing rope, the more closely it resembles bungee jumping.
In this study, the displacement of a spring resulting from the application of forces of varying magnitudes was measured. The validity of Hooke’s law was verified by plotting the resulting displacements as a function of the force exerted upon the hanging spring. Oscillatory motion was also observed, with periods proportional to the square root of the mass attached to the spring.
Transcript
Hooke’s Law and the phenomenon of simple harmonic motion help in understanding the physics associated with elastic objects.
Hooke’s Law implies that in order to deform an elastic object, like a slingshot, a force must be applied to overcome the restoring force exerted by that object. This restoring force is a product of the elasticity constant k of the object and the displacement Δy but in the opposing direction to the displacement or applied force.
Clearly the elastic object stores energy that has the potential to do work. After the work is done the elastic object undergoes oscillation. If we plot this oscillatory behavior as the object’s position versus time, then the graph represents simple harmonic motion.
In this video, we will demonstrate an experiment that uses springs and weights to validate the concepts behind Hooke’s law and simple harmonic motion.
Before demonstrating how a spring behaves, let’s revisit the concepts behind its oscillation. Imagine, applying a force to the spring, like a weight, that causes it to stretch from its initial non-deformed position until an opposing restoring force eventually balances it and equilibrium is established.
As per Hookes’ law, this restoring force is equal to the spring constant k, which depends on the elasticity or stiffness of the material being deformed, times the displacement of the spring from its initial position, or Δy.
Therefore, knowing Δy and recalling that the restoring force is equal and opposite to the applied force, which is the weight in Newtons, the spring constant can be determined. Also, plotting F-applied versus Δy gives a line passing through the origin with a slope that represents k.
Now, with the spring at its equilibrium position, if you introduce an external force and lift the attached weight to a certain height, you allow the spring to gain some elastic potential energy PE. This potential energy is given by this formula, where k is the spring constant and Δy is the distance from the equilibrium position.
Now when you release the spring, it undergoes a periodic motion, known as simple harmonic motion. If plotted on a graph of position versus time, the motion yields the sinusoidal waveform of simple harmonic motion.
The period of oscillation T is given by this formula, which shows that T is inversely proportional to k — the elasticity constant, and directly proportional to m — the mass of the weight attached. Therefore, the larger the mass, the longer the spring would take to complete one cycle of oscillation.
If this system was isolated – unaffected by external forces, the oscillations would go on indefinitely as the kinetic and potential energies, KE and PE, would be continuously converted to one another. But in the real world there are always some frictional forces that cause damping and therefore the spring will ultimately come to a halt.
Now that you have an idea about the laws that govern spring oscillation, let’s see how to test them in a physics lab. This experiment consists of a spring with a known spring constant, a stand, a set of weights with different but known masses, a meter stick, and a stopwatch.
Secure the stand to a solid foundation, such as a table. Attach the spring to the stand making sure there is enough room to stretch the spring without contacting the top of the table.
Using the meter stick, note the non-deformed position of the spring, or the distance between the bottom of the spring and the tabletop. Make a note of this starting position on the meter stick.
Now, starting with the smallest mass, calculate and record its gravitational weight. Attach the weight to the spring and measure the distance between the bottom of the spring denoting the equilibrium position and the starting position noted earlier. Record this displacement value.
Next, raise the weight slightly from its loaded position and release it to observe simple harmonic motion. Using the stopwatch, measure the oscillation period by dividing the time required for multiple periods by the number of periods. Repeat this procedure three times to obtain an averaged period. Since the period does not depend on the amplitude of oscillation, the values should be consistent.
Repeat the measurements of the spring displacement and the oscillation period for each additional weight, in order of increasing mass, and record all the readings.
Using the values from the displacement measurements, plot the gravitational weight as a function of the displacement distance. As expected from Hooke’s Law, the dependence is linear and the slope of the line gives the spring constant. Comparing this measured value to the known spring constant value of k = 10 N/m reveals good agreement to within the error expected for this type of measurement.
Now calculate the potential energies for each weight using the known spring constant and the measured displacements. Given the equation, a plot of potential energy versus displacement square demonstrates linear proportionality.
Using the known spring constant, calculate the oscillation period for each weight. A comparison with the measured periods reveals strong agreement and confirms the expected relationship; that is, the period is proportional to the square root of the mass.
The restoring force that an elastic object exerts when it is deformed can be observed in several everyday events.
The suspension of modern vehicles consists of shock absorbers, which help minimize impact when driving over rough roads. The shock absorbers act as damped springs, absorbing the kinetic energy at impact and then dissipating it. Reducing the spring constant makes the ride smoother or mushier while increasing it is preferred in high performance vehicles for better handling.
Another application of these concepts would be harmonic oscillators – systems that undergo simple harmonic motion and experience continuous energy exchange. For instance, mechanical clocks convert potential energy stored in a torsion spring into mechanical energy to drive the gears and move the hands of the clock. Another example would be an LC circuit, which exhibits oscillation between electric potential energy, stored in the capacitor C, and magnetic potential energy, stored in the inductor L. This oscillation happens over a very specific period given by this formula, making LC circuit an integral part of many electronic devices.
You’ve just watched JoVE’s introduction to Hooke’s Law and Simple Harmonic Motion. You should now understand the concepts of the elastic potential energy, the restoring force, and how this force results in simple harmonic motion. Thanks for watching!
