- 00:07Overview
- 01:15Principles of Standing Waves and Simple Harmonics
- 04:15Observing the Superposition of Wave Pulses
- 05:39Measuring Frequency of Standing Waves
- 06:37Data Analysis and Results
- 07:50Applications
- 09:05Summary
定在波
English
Share
Overview
ソース:アリアナ ブラウンAsantha Cooray 博士は、物理学教室 & 天文学、物理的な科学の学校、カリフォルニア大学、アーバイン、カリフォルニア州
定在波、または停滞性波動が伝播していないように見える、反対方向に同じ周波数と振幅の 2 つの波の干渉によって生成される波。これらの波はない直線的な動きで上下に振動する表示され、マンドリン ギターの弦、湖の水や部屋の空気のような有限のメディアを振動に最も簡単に識別されます。たとえば、文字列は両端固定、長さに沿って旅行 2 つの同じ波が送信される場合、最初の波が終わりバリアにヒットし、反対の方向に反射し、2 つの波が定在波を生成する superpose。この動きは、媒体の長さによって定義される周波数と周期、単振動する運動の視覚的な例です。簡単な調和運動は振動、定期的な運動、意味遠い何かを押すと、一生懸命それを押し戻す復元力は、変位に比例します。
この実験の目的は、波の重ね合わせと定在波を作成する反射の役割を理解し、最初のいくつかの共振周波数の計算にこれらの概念を悪用または高調波、定在波セクシーに。オブジェクトを生成する各周波数が独自の定在波のパターン、最も低い可能な周波数の波が基本周波数と呼びます。調和は、整数番号で基本周波数に比例周波数を持つ波です。
Principles
Procedure
Results
| Harmonic (n) | # Cycles | Total Time (s) | Frequency (Hz) | f/f0 | Period (s) | Wavelength (m) |
| 1 | 10 | 19.2 | 0.521 (f0) | 1 | 1.210 | 16 m |
| 2 | 10 | 9.75 | 1.026 | 1.97 | 0.975 | 8 m |
| 3 | 10 | 6.21 | 1.601 | 3.07 | 0.625 | 5.33 m |
Table 1: Section 2 – Stretched Spring Length = 8 m
In Section 1, principles of wave superposition and reflection in a finite medium are demonstrated and confirmed as pulses were sent down the length of the slinky. Specifically, we see that when two waves with identical amplitudes and phase meet, they undergo constructive interference and their amplitudes add. Similarly, we see that when two waves with opposite polarity (180 ° phase shift) and identical amplitudes meet, they undergo destructive interference and their amplitudes cancel. The latter of these principles is key in understanding standing wave patterns.
In Section 2, the nodes and antinodes of the slinky were easily visible at various frequencies. As the number of nodes increased, so did the frequency. The wavelength is inversely proportional to frequency, so there is naturally a decrease in wavelength. The frequencies of the harmonics are positive integer multiples of the fundamental frequency that correspond to n. For example, using the n = 2 harmonic, the frequency is measured and defined as the number of cycles per unit time:
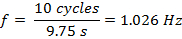
The period is defined as the inverse of the frequency (Equation 2) and is equal to:
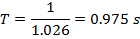
The wavelength is defined in Equation 1 as:
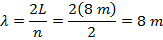
Finally, we can see the integer-proportional relationship between the harmonics and the fundamental frequency by calculating:
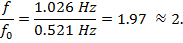
Applications and Summary
In this experiment, the concepts of wave superposition and standing waves were explored in two demonstrations. Wave reflection and constructive versus destructive interference were visualized in the first demonstration. In the second, the changes in frequency and period were measured and higher harmonic frequencies were found to be integer multiples of the fundamental frequency.
A famous example of standing waves in the real world are the strings on a guitar, or any string instrument. In these instruments, a plucked string emits a particular frequency depending on how taut and dense the string is and the string length. Each string only makes certain notes because only certain standing waves, or harmonics, can form on that string. The musician can use their fingers to shorten the string length, creating a new node and new set of harmonics that are proportional to the fundamental frequency. Vibrations that are not at the right frequency, say fingers pinning the strings down onto a fret that doesn't allow for a standing wave at that string length, will sound odd and eventually cancel themselves out.
Standing waves also occur in nature, often in bounded bodies of water like lakes and harbors. Sometimes, they can form on a river bed allowing river surfers to ride this wave for an extended period of time without actually moving. Typically, they form when a large amount of water is flowing over an obstruction, like a big rock, at a rapid pace. As the water flows over the rock and crashes behind it, it creates a large wave in the opposite direction of the river's current that interferes with the incident wave of water. Thus, a standing wave is formed and river surfers can ride it for as long as their balance will allow them since the wave likely will not end in a matter of seconds.
Transcript
Standing waves, or stationary waves, are waves that appear to not propagate and they are most evident in a vibration. For example, when a taut string is plucked, the resulting waves appear to vibrate up and down, with no linear movement. These are actually produced by the interference of two waves traveling in opposite directions, with the same frequency and amplitude.
This oscillating motion with periodic frequency is an example of simple harmonic motion. The motion happens because the string has a restoring force that is proportional to the initial displacement. This relationship between restoring force and displacement is given by Hooke’s Law — explained in detail in another JoVE Science Education video. This essentially means that the harder something is pulled, like this sling shot, the harder it pushes back.
In this video, we will create standing waves using a slinky, and explore the physics behind simple harmonic motion and its applications.
Before we start the demonstration in the laboratory, let’s learn a bit more about standing waves and simple harmonic motion. A wave is defined by its wavelength, lambda — the distance between two crests, and its frequency, f — the number of occurrences of crests in unit time, The amplitude is the distance from crest to trough. When two waves arrive at the same point in a path, at the same time, they interfere. The amplitude of the resulting wave is the sum of the amplitudes of the two waves.
Constructive interference occurs when the amplitudes of the waves are in phase, and add. Destructive interference occurs when the waves are out of phase, and the amplitudes subtract.
Take for example, a pulse on a finite string. Ideally, when the traveling pulse meets a boundary, it is reflected. Now let’s send a wave down the string, and let it reflect back and forth for an extended period of time. This action creates a stationary pattern, or standing wave.
The points of minimum amplitude, called nodes, are where the waves have opposite phases and cancel each other out. The points of maximum amplitude, or antinodes, are points where the waves have the same phase and their amplitudes combine. The simplest standing wave occurs when the wavelength is twice the length of the string.
The next possible standing wave has a node in the center, and the wavelength equals the length of the string. If we continue to add nodes, we create waves with shorter and shorter wavelengths. These patterns are called harmonics, where the number of antinodes, denoted by letter n, gives the wave of nth harmonic. So if the wave has four antinodes, the wave is the fourth harmonic.
Based on the relationship between the wavelength and the length of the string of each harmonic, we can derive a formula relating these three terms and say that lambda of an nth harmonic standing wave equals two times the length of the string divided by n.
Since 2L is the wavelength of the first harmonic, the wavelength of each harmonic is Λ1 divided by n. Now, we know that Λ and f have inverse relationship. Hence, we can deduce that the frequency of each harmonic would be the nth multiple of the first harmonic, or the ratio of the frequency to the frequency of first harmonic yields n. Note that the first harmonic is also known as the fundamental frequency of that string.
Now that we’ve discussed the basics of simple harmonics, let’s take a look at how to make standing waves using a slinky, and how to measure the frequency of standing waves.
First, stretch a slinky or steel spring lengthwise across the floor with one person holding each end. Use tape to mark two lengthwise barriers, each about a foot away from the middle of the slinky, on each side.
Also, add lengthwise barriers that are two feet away from the middle of the slinky on each side.
Take turns for launching wave pulses by jerking the slinky a small distance horizontally, and then immediately snapping it back to the starting point. Ensure that the amplitudes stay within the marked barriers.
Next, simultaneously launch identical pulses with the same polarity, and observe what happens when the pulses meet. The superimposed wave should double in amplitude, cross the first taped barriers and hit the second taped barriers.
Now, simultaneously launch identical pulses with opposite polarity. The pulses should cancel one another out as they superimpose and continue traveling. They should never reach the barriers.
Finally, fix one end by holding it tightly in position. Send a single pulse down to the fixed position, and observe the waves amplitude as it is reflected. It will reflect back with opposite polarity.
Now let’s take a look at how to measure the frequency of standing waves. Stretch the slinky across the room again, and measure the stretched length.
With one end fixed, gently begin sliding the other end horizontally until you find the first harmonic. For this harmonic, there should be only one wave’s crest with one amplitude moving back and forth.
Use a stopwatch to record the time it takes for each wave cycle. One complete cycle starts when an antinode forms on one side, slides through the center to form an antinode on the other side, and then returns to the original position.
Now, increase the speed of the sliding until you reach the next harmonic. For the second harmonic, there should be two wave crests on opposite sides moving in opposite directions. Measure the time for one wave cycle.
Repeat these steps for the third harmonic.
Now that we have discussed the experiment, let’s learn how the analyze the data collected in order to obtain the frequencies of different harmonics. Recall, the wavelength is equal to two times the length of the slinky divided by n. Thus, for the second harmonic, the wavelength is the length of the slinky, or 8 m.
Frequency is defined as the number of cycles per unit time. Thus, frequency can be calculated for each harmonic by dividing the number of cycles by the total time. It is evident that, as n increases, the frequency of the wave also increases.
This was noticeable during the experiment as well. Now let’s verify the relationship between the frequencies and n. If we divide the frequency of each harmonic with the fundamental frequency, then we obtain these values. These values demonstrate that the second harmonic is approximately twice the frequency of the fundamental frequency and the third harmonic is thrice the fundamental frequency. Together, these results validate the harmonics formulae.
Standing waves can be found in many real world examples in science and nature.
A plucked guitar string is a simple example of a standing wave. A plucked string emits a particular sound frequency depending on the string length and how taut or dense the string is.
Each string only makes certain notes because only certain standing waves are able to form on that string. These standing waves are all integer multiples of the string’s fundamental frequency. The musician can shorten the string length, creating a new set of harmonics.
Acoustophoresis, which means migration with sound, is a technique in biomedical engineering that uses standing waves to displace particles in a microscale channel of flowing liquid. This is typically performed in a microfluidic device, which has micrometer scale fluid channels.
When a standing wave with specific frequency is formed within the channel, which focuses the particles into a controlled stream. Using this method, a researcher can rapidly focus or separate microscopic entities.
You’ve just watched JoVE’s introduction to standing waves and simple harmonic motion. You should now understand the properties of standing waves, and where they are present in every day applications. Thanks for watching!
